Introduction

When talking about the “scalability” of blockchains, it’s always good to define first what exactly we mean by it. In this article, I will not focus on things like “how many transactions can be processed by a chain per unit of time”. Instead, I am more interested to explore how we can scale the number of nodes in the system, while still keeping it decentralized and trustless. This problem might sound as an easy one to solve, but as you will see, it’s actually quite a tricky problem.

The structure of this article will be like this:

• First, I will describe some fundamental concepts that one has to know before understanding the problem and the solution proposed by this article. I will describe what full nodes are, what Simplified Payment Verification (SPV) is, how it works, and how Merkle trees are used in blockchains.
• In the second part of the article, I’ll explain the two different implementations of SPV. I will also explain the shortcomings of both variants. Note: Eventhough other chains, such as Ethereum, use Patricia trees, instead of Merkle trees, and use an account-based model, instead of an UTXO model, the same issues hold true for Ethereum as well.
• In the last part of the article, I’ll introduce a possible solution to the scalability shortcomings of SPV. Here I will introduce the idea of an Interactive Bloom Proof (IBP), an interesting concept I came up with while researching at Bloom Lab. It allows for decentralized, truly trustless SPV-like interactions (something that, as we will see, is not possible today), while at the same time allowing the network to scale easily. One can actually build a whole new blockchain architecture around the IBP concept, but that’s a topic for another time. As implementing the Interactive Bloom Proof into existing chains requires hard forking them, I do not expect this idea to get much traction. But I think it is a very useful concept to people working on new blockchain designs.

Full Nodes and Simplified Payment Verification

A device that connects to a blockchain network is referred to in the blockchain space as a “node”. Nodes can be classified as either “full nodes”, or “lightweight nodes”. Full nodes store every block and transaction of a blockchain and constantly check the validity of incoming messages. Full nodes independently create a chain by following some consensus rules. In the case of Bitcoin and (as of this writing) Ethereum, Proof of Work (PoW) is the consensus algorithm used for creating the chain, aka decentralized ledger. Consensus algorithms are quite a large topic and deserve a whole article for themselves. As for this article, if you are not already familiar with PoW, just keep in mind that it’s the algorithm that guarantees that every full node will end up with the same locally stored chain. In other words, thanks to PoW and the chain’s validity rules, full nodes will converge to the same blockchain state, without having to trust anybody. That said, not many users use full nodes to access the blockchain however. Due to the large storage capacity blockchains require (in the case of Bitcoin, as of this writing one needs approximately 302 Gb, and Ethereum’s “archive nodes” more than 4 Tb) most users opt-in with lighweight nodes, or some centralized service.

Lightweight nodes rely on something known as simplified payment verification (SPV). SPV was initially proposed in the original Bitcoin whitepaper and is quite straightforward as a concept: Instead of making nodes download every block in a blockchain, a lightweight node downloads only the block headers. That way, instead of having to store every transaction, one simply stores the previous block hash, a nonce (a value needed for PoW, and a Merkle root (a specific hash). This alone cuts the storage costs significantly. Having locally stored the block headers of a chain, a lightweight node can easily prove if a transaction really occurred by requesting a Merkle proof, also known as a Merkle path.

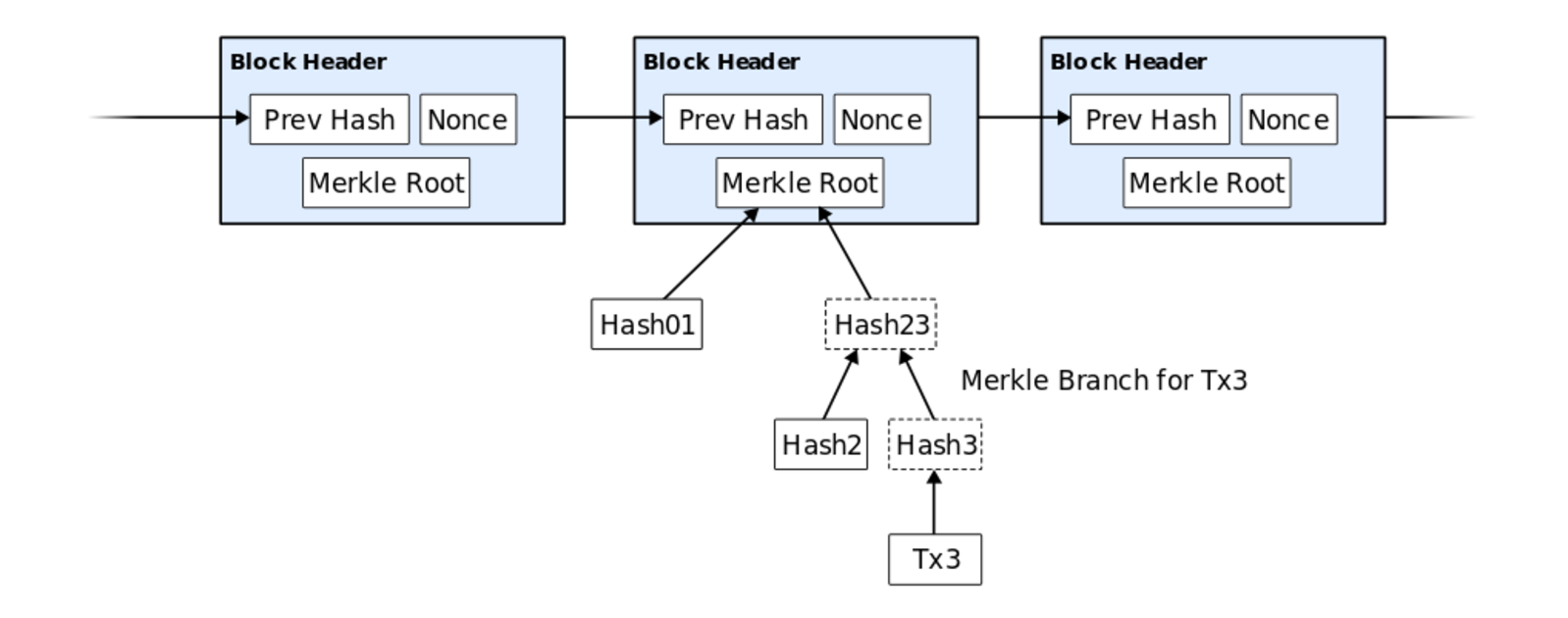
Figure 1. An illustration of how block headers are structured. Taken from the Bitcoin whitepaper.

To understand what exactly a Merkle root and a Merkle proof really are, we have to know how a Merkle tree works. A Merkle tree is a binary tree in which all leaf nodes (i.e. the Merkle tree’s elements, i.e. the block’s transactions) are associated with a cryptographic hash, and all none-leaf nodes are associated with a cryptographic hash, that is formed from the hashes of its child nodes, as shown in figure two.

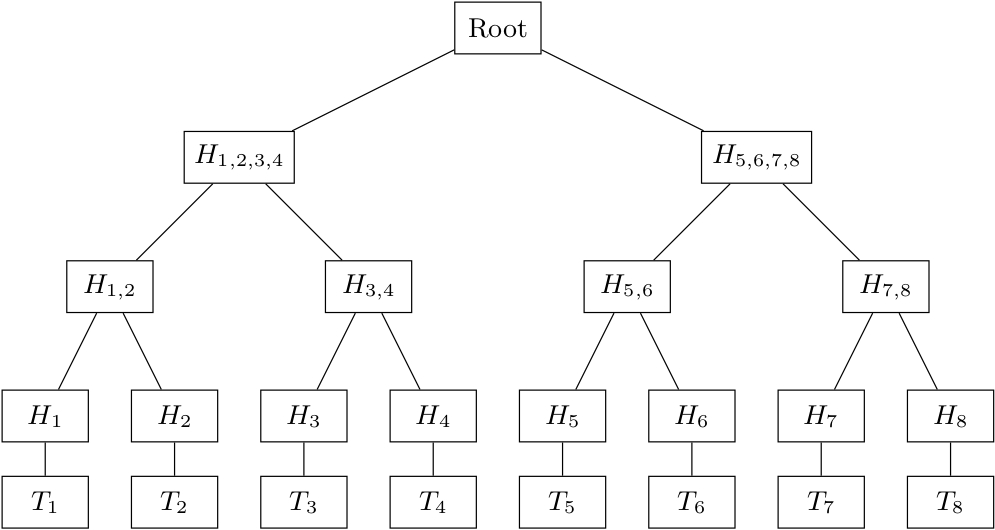
Figure 2. An illustration of Merkle tree. The leaf nodes represent a block's transactions. After the hashing process, a root hash is generated, also known as a Merkle root.

Now when a lightweight node wants to know if a transaction really occurred, instead of having to request all block transactions to generate the block hash, one simply needs a subset of the hashes, as shown in orange in figure 3. Having those hashes, and having the block headers stored locally, a lightweight node can recreate the Merkle root and thus know if a transaction really occurred.

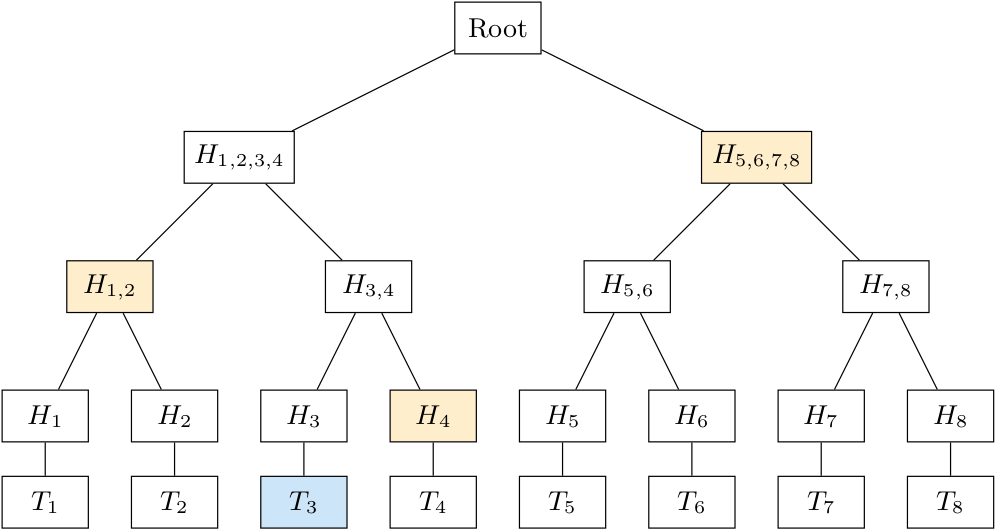
Figure 3. An illustration of Merkle tree and a Merkle proof (shown in orange) for a given transaction hash (shown in blue).

And that’s all simplified payment verification really is. It’s a neat idea that allows the casual user still to participate in a blockchain network, without having to download hundreds of gigabytes and validate every transaction for themselves. There is though a catch that makes today’s SPV less useful than people might think.

The shortcomings of SPV

Back in 2019 there was a lot of fuss on Twitter around chapter 8 of Bitcoin’s whitepaper, the chapter that introduces the concept of SPV. It turned out that different people define the implementation of SPV differently. For convenience, for figure 4., I am going to use Donald Mulders’ illustration from his blog post to clarify the difference.

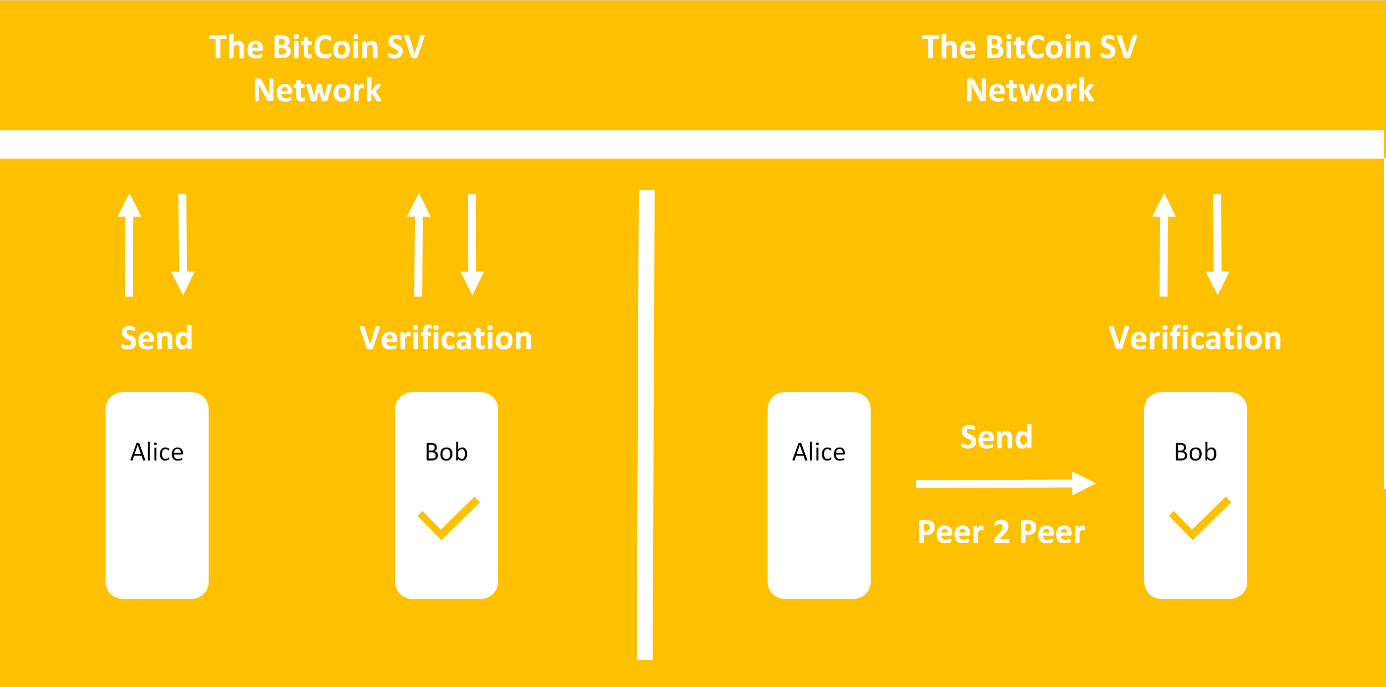
Figure 4. Two ways how SPV can be implemented.

The left model visualizes how most SPV implementations work today. Alice sends a transaction to the blockchain network, it gets included to the chain, Bob can verify that it was included, and he can see that other blocks are added on top of Alice’s transaction. Bob cannot validate the transaction for himself, but as long as the honest nodes represent the majority in the network, he can know that Alice’s transaction was validated and inserted to the chain by the network’s full nodes. Unlike Craig Wright’s claims, it’s quite clear that the left model was originally described in the Bitcoin Whitepaper. Below is a screenshot of the part of the paper for you to read and compare it for yourself with the two models shown in figure 4.

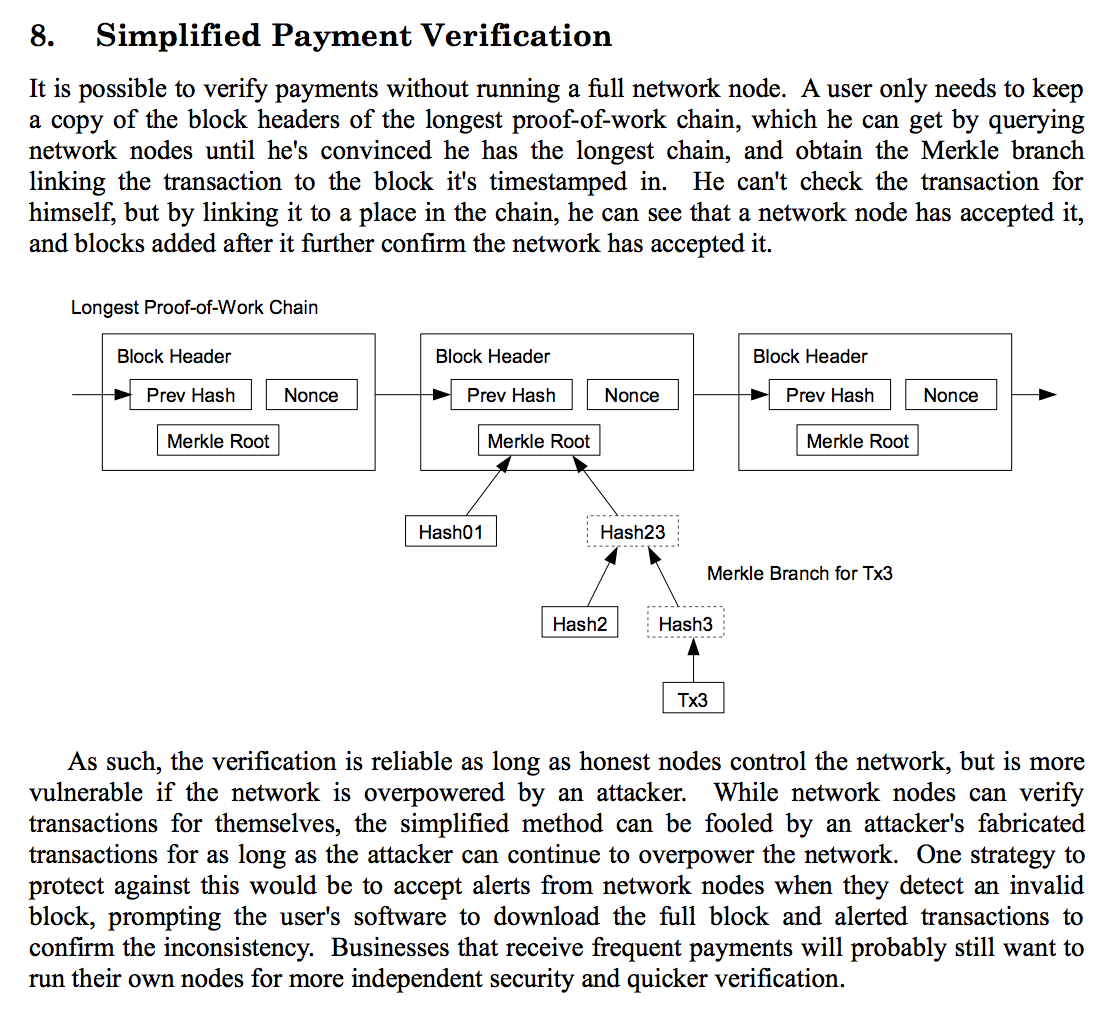
Figure 5. Screenshot of chapter 8 of the Bitcoin whitepaper.

The second model (the model on the right of figure 4) is the model that Craig says is what he really meant when “writing the Bitcoin whitepaper”. Here, instead of Alice having to be connected to the blockchain network, she can simply spend her transaction directly with Bob. Bob can then send the transaction to the network and check if it’s valid. Before criticizing this model, I first want to mention it’s advantages: In this model, Alice does not have to be connected to the network at all to spend her coins. This is quite a huge advantage in my opinion. She can simply send the transaction, as well as the necessary Merkle paths to Bob directly, she doesn’t even have to have an internet connection necessarily. Bob can then check if the right Merkle root of a block header can be created from Alice’s spent transaction(s) and provide the service / product to Alice right away. Bob can then send the transaction to the network for it to be included in the chain. He is in fact incentivized to transmit it to the network as soon as possible, as Alice might spend the same coins later somewhere else.

But wait, according to the model in figure four, there’s also a verification step Bob has to perform with the blockchain network. Well, and that’s where the catch with the right model is. In SPV, even if you get a correct Merkle proof that “locks” a specific transaction with a block header, there’s no way for the lightweight node to know if that transaction was already spend or not. To clarify this last statement a bit, imagine let’s imagine a scenario with Alice and Bob again. Alice received some bitcoin at block number 1000. She then spent her coins at block 1010 for some reason. Now let’s say Bob is a lightweight node following Craigh’s model from figure 4 (the one at the right). Alice could fool Bob by sending him the Merkle proof of the already spent coins from block 1000. Bob would receive the proof, see that Alice really had that many coins at block 1000, and accept it as true. SPV can only show that a transaction really occurred in the chain, it cannot prove that it is still unspent. That’s why in this model, Bob has to communicate with a number of nodes and get their validation that the transaction is unspent. This however is done in a trustful way, i.e. Bob has to contact a bunch of full nodes and hope that the majority will be honest. Note, this is only the case if the chain is based on a UTXO model, an account-based model, like in Ethereum, Bob could get the proof of Alice’s latest account state. Craigh’s model then is not really trustless, and of course he knows that. That’s why he will often say things such as “It is important to note that network miners act within the law” and “It is so because Bitcoin is not designed to be a system that acts outside of the controls of law”. This kind of thinking though doesn’t really align well with the “crypto ethos”. It might just be me, but I don’t really see what’s the point of having all the cryptographic intermediary steps, if at the end of the day you still need to trust full nodes in a non-cryptographic way.

Now that this is out of the way, let’s focus on the interesting things: Thee scaling issues of the original SPV (the left one in figure 4, i.e. the one that was really presented in the Bitcoin whitepaper). Jameson Lopp has a great article about SPV’s scaling issues. The fundamental problem boils down to this - SPV are very efficient for lightweight nodes, but not for the full nodes. As quoted from Lopp’s article:

“Every SPV client must sync the entire blockchain from the last time it had contact with the network, or, if it believes it missed transactions, it will need to rescan the entire blockchain since the wallet creation date. In the worst case, at time of writing, this is approximately 150GB. The full node must load every single block from disk, filter it to the client’s specifications and return the result”.

Ergo, there’s a top ceiling (quite a low one in fact) for how many lightweight nodes can be in the system. Please refer to Lopp’s article for concrete numbers. The fact of the matter is, that with today’s architecture setup, full nodes can simply not serve the increasing number of lightweight nodes. It’s not only a matter of incentives (which is also a problem, but one that is easier to solve), it’s a matter of connectivity. The network of full nodes would simply get clogged. Since lightweight nodes can further be lied to by omission, they have to contact multiple full nodes, making the scalability issue even worse.

To promote easily user onboarding, a concept like that of SPV is crucial. Not everyone can, or even wants to run a full node. We need thus a system that preserves the convenience of SPV, but removes the load from full nodes. Having such a setup would allow a blockchain network to grow in size with fewer network restrictions. But for this we’ll need a whole new architecture, and that’s where the Interactive Bloom Proof comes in.

The Interactive Bloom Proof (IBP)

Full Nodes 2.0

I mentioned Craigh’s model before, because it’s an interesting design, even if it has its flaws. If lightweight nodes could interact with other lightweight nodes, and prove that some coins really belong to someone (as in SPV), while at the same time knowing that the coins are still unspent (something not possible in SPV), that would solve parts of the scalability issue. Before being able to explain the necessary changes we have to make to the blocks of a blockchain for this idea, we’ll first have to know how a Bloom tree works. For anyone interested to know more about the details of the Bloom tree, I’d recommend reading the original paper. It’s a simple concept, but one has to be familiar with both bloom Filters and Merkle trees. If you’re not familiar with bloom filters, please read the first page of the paper. The Bloom tree has an interesting property: It allows for probabilistic presence proofs and non-probabilistic absence proofs in a bandwidth efficient and secure way. In other words, just as in Bloom filters, a Bloom tree can either tell us that an element might be in a set (i.e. false positives are possible), or that it definitely is not in the set (i.e. false negatives are not possible). As we will see, the false positive nature of Bloom filters will not hinder us in any way.

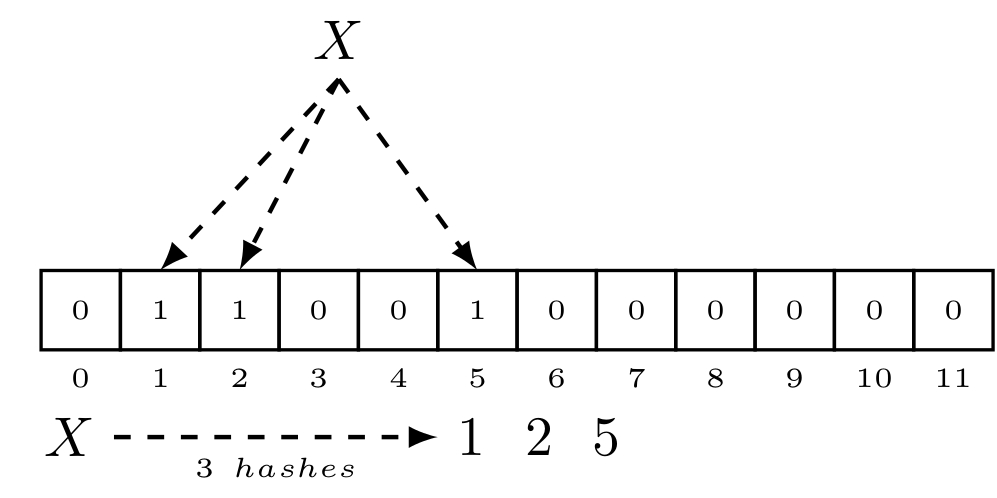
Figure 6. Illustration of how a bloom filter is populated. An element is hashed k times, and the appropriate indices get switched from zero to one.

For the IBP to work, whenever full nodes build a new block, they also build an empty Bloom filter with predefined parameters and populate it with every transaction that was spent in the given block. In the case of the unspent transaction output model (UTXO model), older transactions get unlocked and consumed to create a new transaction. While a block’s Merkle tree gets constructed through the newly created UTXOs, this Bloom filter gets populated by the transactions that just got consumed. Unlike regular Bloom filters, the way we populate this Bloom filter is a bit different: Instead of hashing every spent transaction hash k times, we compute h(t,c) k times, where h can be a non-cryptographic hash function like murmur, t is the transaction hash, and c is a counter. I will get back to this counter in a moment. Once we have populated the Bloom filter with all the spent block transactions, we can build a Merkle tree on top of it. This is essentially what I am referring to as a Bloom Tree. The github implementation divides the Bloom filter into 64 bit chunks, which then are repeatedly hashed to create the tree. It also uses a Compact Merkle Multiproof for more space efficient Merkle proofs.

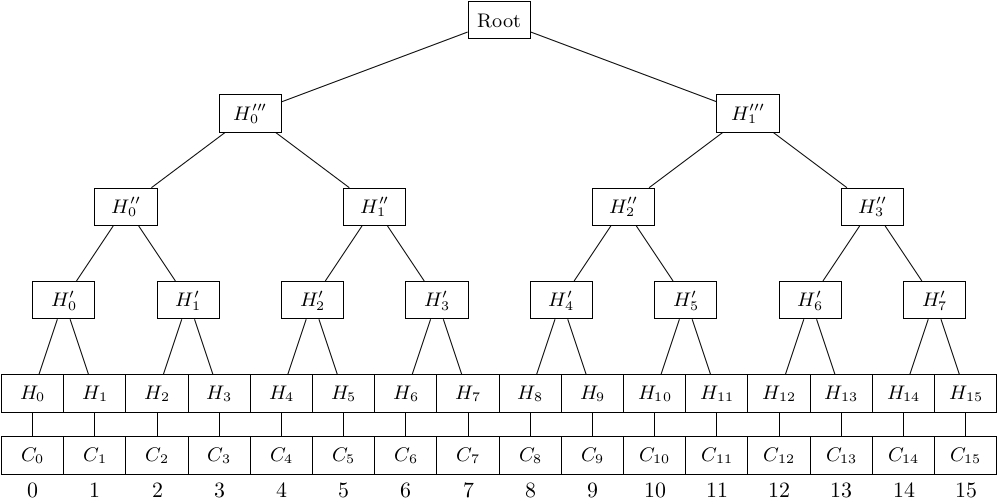
Figure 6. Illustration of a Bloom tree.

With this simple structure, we can provide absence proofs (i.e. show that a transaction did no occur in a block), or probabilistic presence proofs (i.e. show that a transaction might have occurred in a block). For e detailed explanation of the proofs, please refer to the paper, it’s quite an easy read. Now getting back to that counter used to populate the Bloom filter - We will actually not create only one Bloom Tree for a block, but N Bloom trees, each with a different counter, from 0 to N (this will make sense in a moment). This will result in N Bloom filters, each independent of each other, and each with a different mapping (i.e. the bits of the bit array differ for each of the N Bloom filters). The roots of the Bloom trees are then added to the block header (or depending how large N is set, a conventional Merkle tree can be built on top of the Bloom tree roots, and we can insert that Merkle root instead). We can then use PoW to insert the block into the chain, and the Bloom filters can be discarded. To recap, a block header in this setup has all the same components as before (even a regular Merkle root built from the block transactions), but it will also have a Merkle root built from the N Bloom tree roots, which were built from the N Bloom filters, which were populated with the block transactions. The size of N will depend on the parameters of the bloom filters (m, n,k), we will get back to this a bit later.

Bloom Nodes

Ok, up to this point, most of the full node 2.0 setup does not make much sense from the perspective of a full node. Lot’s of computations that slow down block validation, ridiculous. But it enables us to come up with a new node type that allows full nodes to focus on what they’re good at, mining. Let’s call this new node type a Bloom node. You can imagine Bloom nodes as a type of node that is in size between full nodes, and lightweight nodes. Like lightweight nodes, they store the block headers of a chain, instead of the whole blocks. But additionally to that, for every block header, a Bloom node will also store one of the block’s N bloom filters, as well as a Merkle proof that connects the Bloom tree root (which we can compute with the stored bloom filter) with the block headers Merkle root. Which bloom filter gets chosen by a node, gets determined from the Bloom nodes address. If for example Node_address % N returns 4, then that Bloom node will store the Bloom filters that have a counter c equal to four. We do this, because as we will see in a bit, it will be important for the Bloom nodes to know which of its peers has which Bloom filters stored. Now that we have a picture of how the Bloom node is organized, let’s look at an example for how it would operate:

Let’s take a scenario as in figure four (right model). Alice sends Bob directly a coin, as well as a Merkle proof showing that the coin truly belongs to her and occurred in the chain. Bob will check the specified block header and he will see that the coin truly belongs to Alice. Now though, Bob wants to know if the coin is still unspent, without having to contact and trust some full nodes. Bob hashes the UTXO’s consumed inputs k times, and starting from the block header Alice’s coin was referenced at, performs these step iteratively until the latest block header is reached:

• Go to the next block header
• Take the bloom filter that is stored for that block
• Check the state of the bloom filter at the k indices
• If at least one of the bits is zero, you know that Alice’s coin was not spent in this block.
• If all the bits of the bloom filter are set to zero, Alice’s coin might have been spent at this block. Append the block height to a list.

Once Bob iterates over his block headers, Bob will end up with a list of block heights in which Alice’s coin might have been spent. Bob can then ask his peers, who are also Bloom nodes, for absence proofs for those block heights. If all the block heights receive an absence proof, Bob can know for a fact that Alice’s coin was not spent in the meanwhile, and that it really belongs to her. Bob can then send the transaction to full nodes, so that it can be inserted to the transaction pools of the full node network.

If for a specific block height, Bob receives presence proofs from all N contacted peers (each peer would be contacted for a different bloom filter), then Bob can know for a fact that Alice’s coin was already spent. Here it is important to mention that N will ideally should be chosen in a way that results in an astronomically small probability for a false positive. For example, If the false positive rate of a single bloom filter was set to be 0.001, then by having N set to 25, one would have a total false positive rate of 1 x 10^75. Thus, if we were to populate a bloom filter with around 3000 transactions, the size of the bloom filter would be only around 43133 bits (feel free to play around with this Bloom filter calculator), so around one magnitude fewer bits than storing a whole block. By increasing N, one can decrease m further (the size of the Bloom filter). One can of course not increase N indefinitely, as a smaller m means a higher false positive rate for a single Bloom filter, which means having a larger list of block heights that need to be checked with neighboring Bloom nodes.

Something very interesting should be noted here: If a transaction is not spent, proving its “unspentness” will be relatively cheap. We need only a single absence proof from a Bloom filter to know that a transaction was not spent. If on the other hand, a transaction was truly spent and Alice was lying, than Bob would have to collect N presence proofs from his peers, which can be expensive. I will provide a solution to this in the Discussions section, as it’s quite easy to solve in an efficient way. But I will also show why this is actually a feature, not a “bug”, from a scalability perspective.

A ‘Pub Sub’ for Bloom Nodes

One of the good things about the above mentioned procedure, is that Bloom nodes do not have to ask full nodes for the block headers, or even bloom filters. Full nodes could send the block headers + Bloom filters to the Bloom node network, who then can get the block headers + corresponding Bloom filters from one-another. Since Bloom nodes can know that a Bloom filter was part of a block via a Merkle proof, they would simply follow the longest chain rule in a trustless way. At the beginning of the IBP section however, I mentioned that IBP “would solve parts of the scalability issue”. It’s true that Bloom nodes do not have to trust and ask several full nodes to know if a transaction is unspent, but they will still have to periodically contact full nodes to get their UTXOs and the Merkle proofs for those UTXO. Remember, When Alice sent the transaction to Bob, she sent it with a Merkle proof. She will still need to get that information from full nodes. As long as Bloom nodes still have to contact full nodes periodically, the scalability issue remains.

We can overcome this issue however, by using a Kademlia like distributed hash table (DHT) to store the latest UTXOs within the Bloom node network. Whenever a new UTXO gets created, we can store it, together with the UTXOs Merkle proof in the Bloom nodes’ DHT network. The holder’s address could be used as a key, whereas the UTXO and the Merkle proof could be used as values. When Alice comes online, she can simply ask the network for any new UTXOs sent to her address. Spent transactions could be periodically deleted from the network, so that the Bloom node network does not have to store too many additional things.

This way Bloom nodes would not have to contact full nodes at all, allowing for significant scaling. Full nodes would serve as publishers to the Bloom nodes DHT network, while Bloom nodes could “subscribe” to their addresses (or other addresses as well).

Discussions

The problem of having to collect a lot of presence proofs, if a transaction was already spent, is solvable. After explaining how one can solve it however, I will also explain why it might be better to keep it that way. Instead of collecting N presence proofs from the Bloom trees, we could collect a single Merkle proof from the conventional Merkle tree that is used in blocks (the one that is built from the transactions). Done. This way we would require a single Merkle proof for both absence proofs and presence proofs. I don’t find this solution elegant enough however. To get such a presence proof, a Bloom node would have to contact the full nodes network (because the Bloom nodes DHT network would not contain that Merkle proof). We don’t want that.

To prevent a malicious Bloom node to DDoS the Bloom nodes network, we could add rules to remove a peer from one’s peer list, if the peer sends invalid transactions. Another way to prevent malicious Bloom nodes to DDoS the network, would be by forcing the transaction sender to collect the absence / presence proofs, instead of the receiver. There are various ways one can deal with this issue.

Overall, as mentioned at the beginning of the article, I do not expect this idea to get much traction. Hard forking existing chains is always a tricky thing, plus a lot of the modern chains use account-based models. The currently presented IBP proposal would have to be modified to work with an account-based chain (which isn’t that difficult, but again, hard forks suck). I do think though that the Interactive Bloom Proof idea in combination with a pub sub like network, has a lot of potential. I think that we’re still in the early-stage for blockchain architectures. There are still a lot of problems in the current way we build blockchains that need solving. The IBP might be a useful tool in a blockchain engineer’s / researcher’s toolbox.